STM: rng sig inc

ABS: IsRing(T;plus;zero;neg;times;one)

STM: ring p wf

ABS: Rng

STM: rng wf

STM: rng properties

STM: rng all properties

STM: assert of rng eq

STM: decidable rng eq

ABS: CRng

STM: crng wf

STM: crng properties

STM: crng all properties

ABS: r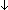xmn

STM: mul mon of rng wf

STM: mul mon of rng wf c

STM: mul mon of rng wf a

STM: mul mon of rng wf b

ABS: r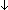+gp

STM: add grp of rng wf

STM: add grp of rng wf a

STM: rng minus over plus

STM: rng minus minus

STM: rng minus zero

STM: rng plus inv

STM: rng plus inv assoc

STM: rng plus zero

STM: rng plus cancel l

STM: rng plus assoc

STM: rng times assoc

STM: rng times one

STM: crng times comm

STM: crng times ac 1

STM: rng times over plus

STM: rng times zero

STM: rng times over minus

STM: rng plus comm

STM: add grp of rng wf b

STM: rng plus ac 1

STM: ring triv

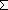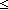ABS: (r) i  k < j. E(k)

STM: rng sum wf

STM: comb for rng sum wf

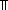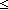ABS: (r) i  k < j. E(k)

STM: rng prod wf

ABS: a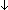+nsgp

STM: nsgrp of ideal wf

ABS: a | b in r

STM: ring divs wf

ABS: r 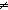 0

STM: ring non triv wf

ABS: IsIntegDom(r)

STM: integ dom p wf

STM: sq stable integ dom p

ABS: IsField(r)

STM: field p wf

STM: any field is integ dom

ABS: IntegDom{i}

STM: integ dom wf

ABS: Field{i}

ABS: r-Prime(u)

STM: rprime wf

ABS: S Ideal of R

STM: ideal p wf

ABS: Ideal(r){i}

STM: ideal wf

ABS: (0r)

STM: zero ideal wf

ABS: (1r)

STM: one ideal wf

ABS: (a)r

STM: princ ideal wf

STM: ideal defines eqv

STM: det ideal ap elim

STM: det ideal defines eqv

ABS: Carrier(r/d)

STM: quot ring car wf

STM: quot ring car qinc

ABS: r / d

STM: quot ring wf

STM: type inj wf for qrng

STM: quot ring car elim

STM: quot ring car elim a

STM: quot ring car elim b

STM: all rng quot elim

STM: all rng quot elim a

STM: rng car qinc

ABS: IsPrimeIdeal(R;P)

STM: prime ideal p wf

STM: sq stable prime ideal

ABS: IsMaxIdeal(r;m)

STM: max ideal p wf

ABS: rng_hom_p(r;s;f)

STM: rng hom p wf

ABS: rng_chom_p(r;s;f)

STM: rng chom p wf

ABS: RingHom(R;S)

STM: ring hom wf

ABS: nat(r;a)

STM: idom alt char

STM: quot by prime ideal

STM: princ ideal mem cond

STM: ideal of prime

ABS: 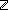-rng

STM: int ring wf

ABS: (i)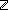-det-fun

STM: int pi det fun wf

STM: int pi detach

STM: prime ideals in int ring

ABS: choose(n;i)

STM: choose wf

STM: comb for choose wf

ABS: e 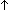r n

STM: rng nexp wf

STM: comb for rng nexp wf

ABS: n 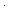r e

STM: rng nat op wf

STM: comb for rng nat op wf

STM: rng nexp zero

STM: rng nexp unroll

STM: rng nat op one

STM: rng nat op add

STM: rng sum unroll base

STM: rng sum unroll hi

STM: rng sum unroll unit

STM: rng sum unroll lo

STM: rng sum shift

STM: rng sum split

STM: rng sum plus

STM: rng times sum l

STM: rng times sum r

STM: rng times nat op

STM: rng times nat op r

STM: binomial

STM: sum of geometric prog

ABS: when b. p

STM: rng when wf

STM: comb for rng when wf

STM: rng times when l

STM: rng times when r

STM: rng when of zero

STM: rng when thru plus

STM: rng when when

STM: rng when swap